Predictability of pharmaceutical spending in primary health services using Clinical Risk Groups
Abstract
Background
Risk adjustment instruments applied to existing electronic health records and administrative datasets may contribute to monitoring the correct prescribing of medicines.
Objective
We aim to test the suitability of the model based on the CRG system and obtain specific adjusted weights for determined health states through a predictive model of pharmaceutical expenditure in primary health care.
Methods
A database of 261,054 population in one health district of an Eastern region of Spain was used. The predictive power of two models was compared. The first model (ATC-model) used nine dummy variables: sex and 8 groups from 1 to 8 or more chronic conditions while in the second model (CRG-model) we include sex and 8 dummy variables for health core statuses 2–9.
Results
The two models achieved similar levels of explanation. However, the CRG system offers higher clinical significance and higher operational utility in a real context, as it offers richer and more updated information on patients.
Conclusions
The potential of the CRG model developed compared to ATC codes lies in its capacity to stratify the population according to specific chronic conditions of the patients, allowing us to know the degree of severity of a patient or group of patients, predict their pharmaceutical cost and establish specific programmes for their treatment.
Keywords
Risk adjustment; Pharmacy expenditure; Clinical Risk Groups; WHO-ATC-Code.
Abstract del artículo disponible en www.healthpolicyjrnl.com
Artículo comlpeto en www.sciencdirect.com
Enero 2014
Authors
David Vivas Consuelo
Research Centre for Health Economics and Management (CIEGS), Universitat Politècnica de València, Cno de Vera s/n, Valencia, Spain.
Ruth Usó Talamantes
Valencian Community Government, Health Department (Conselleria de Sanitat), General Direction of Pharmacy and Pharmaceutical Products, PharmacoEconomics Office, Valencia, Spain.
José Luis Trillo Mata
Valencian Community Government, Health Department (Conselleria de Sanitat), General Direction of Pharmacy and Pharmaceutical Products, PharmacoEconomics Office, Valencia, Spain.
Maria Caballer Tarazona
Faculty of Economics, Universitat de València, Spain.
Isabel Barrachina Martínez
Research Centre for Health Economics and Management (CIEGS), Universitat Politècnica de València, Cno de Vera s/n, Valencia, Spain.
Laia Buigues Pastor
Research Centre for Health Economics and Management (CIEGS), Universitat Politècnica de València, Cno de Vera s/n, Valencia, Spain.
1.Introduction
Pharmaceutical expenditure is nowadays one of the most important and increasing factors in financial terms in healthcare in European countries [1]. Therefore, explaining the variations of expenditure on medicines is of paramount value. Due to the fact that patient complexity is a major determinant of expenditure, methodologies aimed at allocating an average pharmaceutical expenditure by specific patient characteristics are of great use in monitoring the range of prescription of medicines and therefore pharmaceutical expenditure.
There are different grouping systems based on existing administrative and clinical data that can explain and predict pharmaceutical expenditure. Some of these are based on electronic prescription information, such as WHO-ATC and the Rx models [2], [3], [4] and [5]. Others are based on diagnoses: Clinical Risk groups (CRGs) [6] and [7], Adjusted Clinical Groups (ACGs) [8] and Diagnostic Cost Groups, (DCG). Finally there are the mixed models that combine both – Diagnostic Cost Groups, (DCG/Rx) [9] and Adjusted Clinical Groups (ACG/Rx) [10]. The usefulness of these models is especially relevant for integrated health systems such as National Health Systems.
These tools described above also allow stratification of the population according to morbidity, which permits patients with the greatest risk to benefit from case management programmes. This improves the quality of care and life, as this system allows individuating the specific state of health of the population and makes it possible for patients to be introduced into disease management programmes.
This paper focuses on testing the suitability of CRGs for predicting expenditure in pharmacy budget allocation in an Autonomous Community in Eastern Spain. We also show the importance of using local weighting as opposed to standard weighting [7].
2. The Valencian health system and pharmaceutical management
This study was carried out in the Valencia Community (VC) in Spain, where pharmaceutical management is decentralised, being divided into 24 health districts. Each health district receives an annual per capita amount to attend to its assigned population. The flow of incoming and outgoing patients to and from other health districts generates an inter-centre turnover to establish the corresponding economic compensation [11]. The allocated budgets include a specific section for pharmaceutical expenditure that, at present, is adjusted only by socio-demographic variables, such as age, sex and pharmaceutical co-payment. The adjustment was made using a Standardized Amount Indicator built with the above-mentioned variables that allocated a cost per equivalent patient standardized [12]. The predictive level of this model is lower than 15%. This low percentage is basically due to the non-inclusion of morbidity variables, which best serve to explain the behaviour of pharmaceutical expenditure, but nevertheless are not reflected in the current budget allocation for health departments.
Some research exists using different grouping systems for predicting or studying total health expenditures [3], [4], [5], [6] and [13], but we lack research using these methods to focus specifically on pharmacy expenditure [14] and [15].
The adjustment by chronic conditions that CRG classification provides offers a great innovation for pharmaceutical management in allowing the rationalization of pharmaceutical expenditure. The VC has introduced tools over recent years that have the objective of establishing clinical criteria that improve efficiency in pharmaceutical prescription. Given that the clustering criteria of CRG classification is based on unhealthy and chronic conditions, this system provides the doctor with information about the severity of his patients and an adjusted pharmaceutical expenditure forecast. This is only possible with a reliable and comprehensive Electronic Health Record (EHR), where all clinical encounters and coded diagnostics of patients in the different health care system settings are registered [16].
Previously, when a reliable EHR was not available, prescription data and WHO-ATC codes were used to establish the risk adjustment system [17]. However, although this system achieves a high explicative power for pharmaceutical expenditure, it is difficult to operate and has poor clinical use, as it is not connected with the EHR and a regular cross section calculation of weights is necessary. In the VC, the CRG system is in a period of implementation and testing.
2.1. The Clinical Risk Groups
We have chosen Clinical Risk Groups (CRGs) as it is a system that classifies individuals into mutually exclusive categories with clinical significance [18]. Using enrolment data, claims or other encounter level data, this system assigns each person with a chronic health condition to a severity level. CRG classification of the individual is by medical care services used over an extended period of time.
All groups can be classified into 9 statuses from healthy individuals to individuals with catastrophic condition. CRGs (1079 groups) are consolidated into three tiers of aggregation referred to as Aggregated Clinical Risk Groups (ACRGs). The three successive tiers of aggregation are referred to as ACRG1 (416 groups), ACRG2 (151 groups) and ACRG3 (38 groups), with ACRG3 being the highest level of aggregation, consisting of severity adjusted statuses. Each successive tier maintains status and severity levels while reducing the number of groups. Although the aggregation of CRGs reduces clinical precision, it maintains clinical meaningfulness. The ACRGs take into consideration the future medical care needs and clinical similarity of the individuals assigned to them.
The CRG system can be used to understand patterns of health service use and consumption and to develop applications for risk and price adjusting [7], although their use in pharmaceutical expenditure adjustment has not been tested [15]. The main clinical and managerial characteristic is their ability to identify patterns of pharmaceutical consumption in relation to the chronic conditions of a determined patient. For example, should a group of patients with an excessive pharmaceutical cost be identified, it can determine if this is related to the chronic condition they have and help establish corrective measures.
The principal difficulty with the use of CRGs is the need for exhaustive and reliable information on diagnoses and use of health care services over a long period of time (minimum one year). Therefore, when this information is not available, the ATC model may be a suitable option.
To obtain the CRGs we used 3M™ Clinical Risk Grouping Software v.1.4. CRGs capture the resource utilization of all inpatient and ambulatory encounters, identifying individuals with multiple chronic co-morbid conditions and explicitly specifying the severity of illness for each individual.
The main aim of this paper is to test the suitability of the model based on the CRG system and obtain specific adjusted weights for determined health states through a predictive model of pharmaceutical expenditures in primary health care.
In this study, we developed a predictive model based on CRG grouping into 9 health states and the weights for each state were calculated using real data. We used an appropriate comparison system, described in a recent work [17], the ATC-model, a retrospective model that classifies patients according to the number of chronic conditions in 9 groups, from healthy to those with 8 chronic diseases or more and also includes gender.
3. Data and methods
3.1. Data
We used information from a population of 261,054 between January and December 2008, taken from one health district of the VC, which contains 24 health districts connected by a single integrated EHR. Data for each patient included in the study was obtained from the Ambulatory Information System, integrated in the EHR of the Valencia Health Agency of the Generalitat Valenciana (Autonomous Health Department). The Population Information System from the Valencia Health Agency provided demographic information. All case IDs used for data linkage were encrypted according to the data protection law in Spain.
The general practitioner uses an EHR for collected patient health information generated by each meeting in any care delivery setting. It includes patient demographics, progress notes, problems, medications, vital signs, past medical history, immunizations, laboratory data and radiology reports, as well as a specific module for electronic prescriptions that is coded using WHO-ATC codes [19] and the number of defined daily doses (DDD).
The variables considered were: annual pharmaceutical expenditure by patient, gender (1 woman and 0 man), age, pharmaceutical co-payment status (1 for without co-payment and 0 for a co-payment of 40%), 18 groups of ATC-code as proxy for 18 chronic conditions; 9 Health Status of ACRG3 assignment. At the time of the study, Spain had only co-payment for medicines, with two categories of co-payment – pharmacy gratuity for pensioners and population without resources, and co-payment of 40% for others [1].
The grouping system based on prescription and ATC-model considers 9 groups. The first group are persons without chronic conditions, with successive groups up to the 9th depending on the number of chronic conditions from 1 to 8 or more.
Table 1 shows the ATC-code related with each chronic condition and the number of patients who have received at least 5 prescriptions per year. We use a classification of medicines validated by Lamers and van Vliet [4] and modified by Vivas et al. [17].
Table 1. Number and percentage of patients by 18 chronic conditions
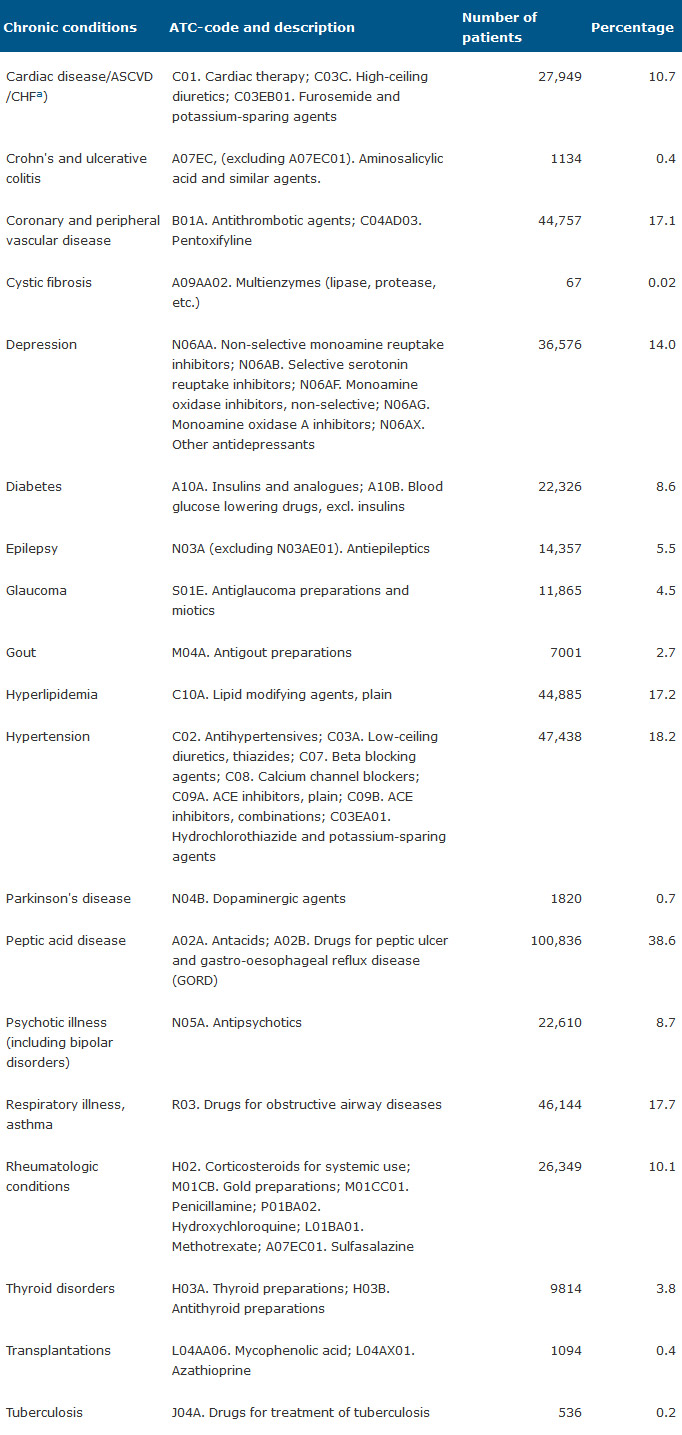
a: ASCVD: arteriosclerotic cardiovascular disease, CHF: congestive heart failure.
3.2. Mathematical models
Two models were developed to explain pharmaceutical expenditure in primary health care. The dependent variable was always the neperian log of annual pharmaceutical expenditure by patient. The logarithm of the pharmaceutical expenditure is estimated as a better approach to its normal distribution of the variable, due the asymmetric probabilistic function of this variable.
Age and co-payment status were excluded due to the high correlation with the chronic condition classification and health status. However demographic variables such as age or gender have a low weight in the models when morbidity variables are introduced [20] and [21]. In both models the healthy group (patients with no chronic disease) was the control variable necessary in the regression model.
As independent variables for the first model (ATC-model) we take the following dummy variables: X1 sex (0 man, 1 woman); X2–X9 variables for groups from 1 to 8 or more chronic conditions:
Y=α+β1X1+β2X2+β3X3+…+β9X9+ε
where α is the constant of the model which corresponds to the weight for a male patient without chronic conditions; β1 is the weight corresponding to sex; β2, …, β9 are the weights corresponding to the number of chronic conditions of the patients; ɛ is the standard error of the model.
In the second model (CRG-model) we also include sex (X1) and from X2 to X9, 8 dummy variables for health statuses 2–9 of ACRG3 assignment:
Y=α+β1X1+β2X2+β3X3+…+β9X9+ε
where α is the constant of the model which corresponds to the weight for a male patient who belongs to healthy group. β1 is the weight corresponding to sex; β2, …, β9 are the weights corresponding to the status 2–9 of ACRG3 assignment; ɛ is the standard error of the model.
The models were estimated by means of ordinary least squares (OLS). The goodness of fit was determined through the corrected R2 value and the F Snedecor, mean squared error, and for each of β coefficients t-Student values were obtained to determine the level of significance. The assumptions of normality, homoscedasticity and linearity were considered.
The statistics to test the multicollinearity was the Condition Number Test. The Condition Number is computed by finding the square root of the maximum eigenvalue divided by the minimum eigenvalue. If the Condition Number is above 30, the regression is said to have significant multicollinearity. Also a formal detection-tolerance or the variance inflation factor (VIF) for multicollinearity was obtained.
The linear regression models allow us to explain the neperian log of pharmaceutical expenditure (dependent variable Y) in function of each considered independent variable (Xi). The mathematical expression is:
Pharmaceutical expenditure = e(α+β1·x1+…+βn·Xn)
4. Results
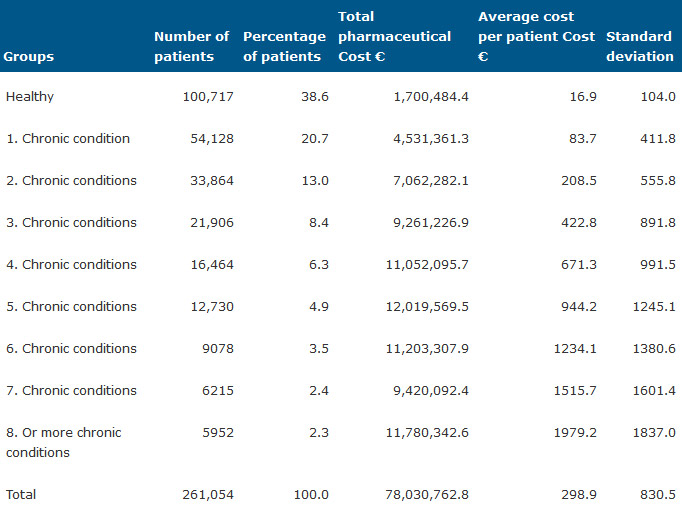
Table 2 shows the number of patients classified using the ATC-model in nine groups from healthy to 8 or more chronic conditions. The percentage of patients logically decreases in relation to the number of chronic conditions from 38.6% in the healthy group to 2.3% in the group with 8 or more conditions. The average cost increases from 16.9 to 1979 Euros. It can be seen that the standard deviation shows a high variability of cost.
Table 2. Patients and pharmaceutical cost by groups of patients from chronic conditions classification.
The grouping results for the CRG system are presented in Table 3. Here, 52.1% were considered as healthy, which is lower than figures reported for this status by other scholars using a less reliable diagnostic codification [22]. The average cost also increased from 42 Euros for a healthy person to 2210 for status 7, though was less than expected for statuses 8 and 9. These groups include malignancies and catastrophic diseases for which patients are treated in hospitals, where consumed medicine is not dispensed in PHCs
Table 3. Number of persons, percentage and average cost by category and CRG severity level.
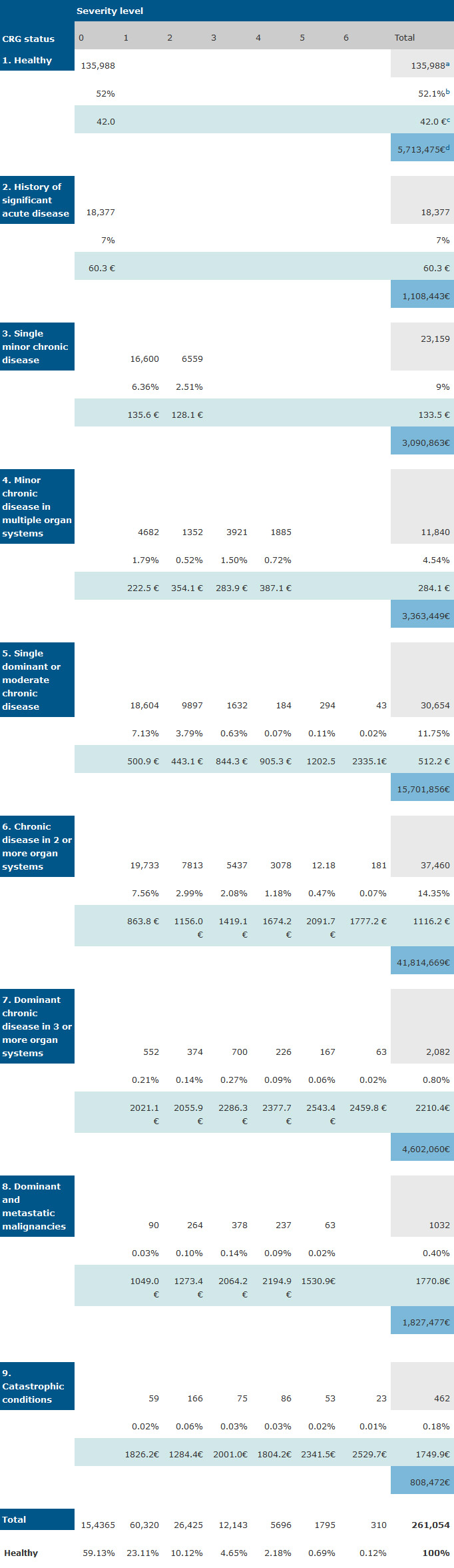
a: number of patients;
b: percentage of patients;
c: average cost per patient of this group; d: total pharmaceutical cost of this group.
The results for CRG aggregation level 3 (ACRG3) are presented (Table 3) including the severity level established in this aggregation for each health status. Two values were calculated for each group, one representing the average cost in pharmacy and the other the number of patients as a percentage of the total. This is the traditional manner of presentation of this assignment level. Thus, Table 3 gives us a picture of morbidity distribution of the population studied.
The pharmaceutical cost observed in certain severity levels of some health statuses do not correlate with weights given in the original theoretical model [7]. No significant difference in number of patient distribution was obtained, except for statuses 4 and 6, where a difference was also observed in severity levels.
The patients of health statuses 5 (single dominant or moderate chronic disease) and 6 (chronic disease in 2 or more organs) represent 26% of the population but consume 57.5 million Euros annually, 73.71% of the total consumption. This is due to these statuses containing the highest number of dominant chronic disease sufferers, such as hypertension, diabetes or hyperlipidemia. It is not possible to infer this type of discrimination with the ATC model.
From a statistical point of view, in the ATC model the total cost of the groups tends to be evenly distributed over the different groups, while the CRG model offers us a classification corresponding more to the clinical reality (Table 2 and Table 3).
With the regression model developed we obtain weights specific for pharmaceutical expenditure, which is the important contribution this paper offers to groups working in this area. The levels of explanation by R2 of both models are similar, with 52.5% for ATC-model (Table 4) and 47.5% for CRG (Table 5), despite the higher complexity of CRG. Small but significant differences by gender are appreciated, with men receiving fewer prescriptions than women on average.
Table 4. Regression model 1 with ATC chronic diseases number of medicines as independent variables.
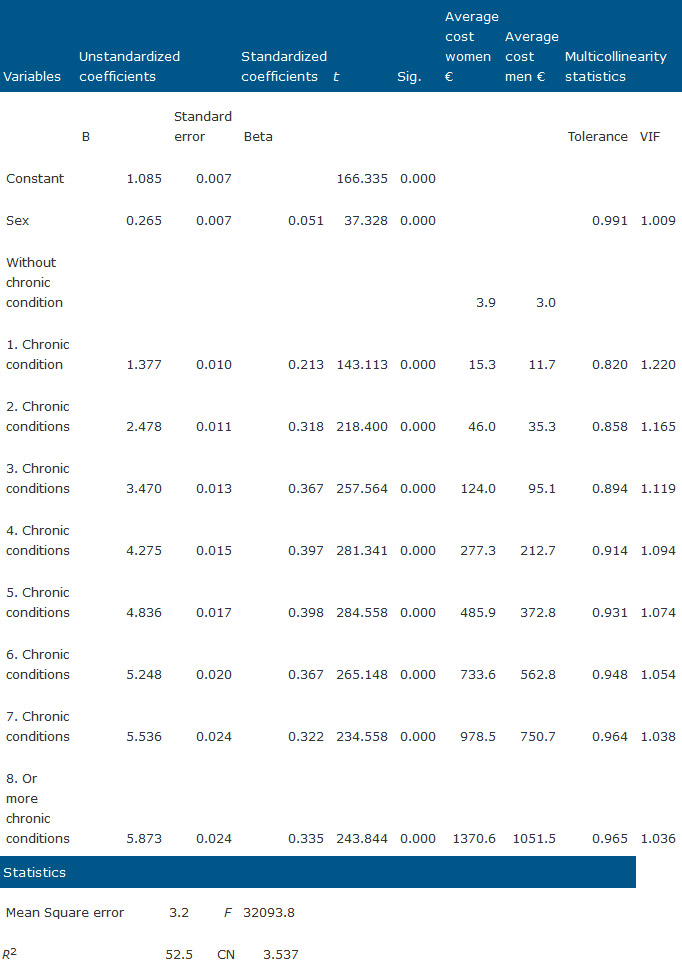
Table 5. Regression model 2 with CRG health statuses as independent variables.
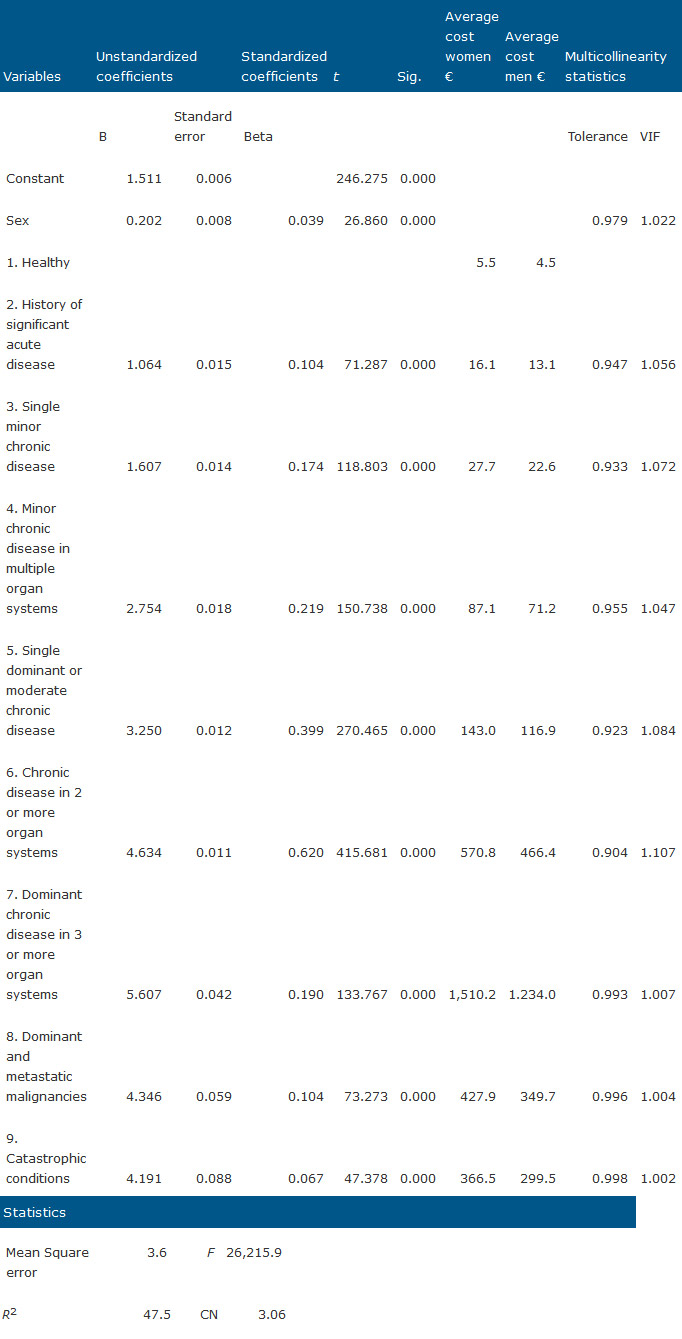
From the coefficients obtained in the CRG model, undoing the neperian log transformation we obtain a standard cost for health status by sex that allows us to establish the specific standard costs for the CRG for pharmaceutical expenditure in primary health care, adapted for the region of application.
5. Discussion
This study is intended to examine the usefulness of CRGs as a method of risk adjustment in pharmaceutical management in primary health care. The validation of its predictive power was made comparing it to a non-hierarchical model using the ATC-model. The predictive power obtained from these two models is 0.525 for the ATC-model and 0.475 for the CRG [15]. Both of these models reach similar levels to those found with ACG [8] and [23] and DCG/HCC [24].
Initial studies found that demographics alone have very low predictive power [10]. The introduction of diagnosis cost group/hierarchical conditions categories (DCG/HCC) greatly improves the predictive power compared to models that use sex and age alone as independent variables [24].
The ACG case-mix system has been used in some PHCs in Spain and validated in a study using data from an entire Canadian province [8]. These authors found that the ACG case-mix system predicted drug expenditure better than the Charlson index of comorbidity. The squared correlation reached from ACGs was 0.24, with the Charlson giving 0.14. On the other hand, a study of Aragon, Spain (n = 84,152) using DxRx-ACG with Spanish case-mix calibration reached 42% of explanation [23].
The ATC-model used as comparison with CRGs is obtained grouping the number of chronic conditions from 1 to 8 or more from data provided by an electronic prescription system. The main advantage is the reliability of data but the clinical significance is poor. This is because it indicates only the number of chronic diseases of the patient and not the specific illness itself, making it impossible to use in programmes for disease management.
The CRG model is more useful from the clinical point of view. In the context of European and the Spanish National Health Systems, the weights obtained in the regression models could be used to establish a pharmacy capitation system in order to assign pharmaceutical budgets to health districts and PHCs. In the V C, the Health Department is developing an interactive computer tool to monitor the pharmacy expenditure from health district to doctor level. Using CRGs the doctor may then identify deviations from the predicted model. Chronic disease management programmes based on CRG patient stratification are also in the process of implementation. We see this as the main contribution in terms of health policy making.
The limitation of the CRG model is that obtaining the information for grouping is complicated. This system is designed for adjusting total health spending, and it would be appropriate to include the hospital pharmaceutical cost in the model. Other, wider studies need to be made of various years, comparing cohorts of patients in order to improve the information and to compare the predictive power.
6. Conclusion
The potential of the CRG model developed using locally specific weights compared to models using to ATC codes lies in its high capacity to stratify the population according to specific chronic conditions of the patients, in such a way that we are able to know the degree of severity of a patient or group of patients, predict their pharmaceutical cost and establish specific programmes for their treatment. As this paper shows that the explicative power of the proposed model is very similar to that of the model used for comparison, this means in practice, and if local weights are used, a highly relevant advance in pharmaceutical management in terms of improving prescription efficiency and management of chronic patients.
Therefore, even though the levels of explanation obtained in both models are quite similar, the CRG model shows some strength from an operational point of view. The explicative capacity of CRG for pharmaceutical expenditure is useful in comparison with the ATC-model, as the ATC-model must be calculated retrospectively from the WHO-ATC Codes prescribed at a specific time, while the CRG model is available in real time, taking the information from the electronic clinical report. In addition CRG model has a greater potential to manage patients with chronic conditions and monitor pharmaceutical expenditure and medicine use.
Although the validity of the predictive power may require further research to refine the model, much of its potential relies on the development of a sufficiently powerful IT tool capable of managing the large amount of information it offers.
Acknowledgements
This study was financed by a grant from the Fondo de Investigaciones de la Seguridad Social Instituto de Salud Carlos III, the Spanish Ministry of Health (FIS PI12/0037). The authors would like to thank members (Juan Bru and Inma Saurí) of the Pharmacoeconomics Office of the Valencian Health Agency. The opinions expressed in this paper are those of the authors and do not necessary reflect those of the afore-named. Any errors are the authors’ responsibility. We would also like to thank John Wright for the English editing.
References
1 L.K. Saastamoinen, J. Verho. Drug expenditure of high-cost patients and their characteristics in Finland. The European Journal of Health Economics, 14 (3) (2013), pp. 495–502
2 D.O. Clark, M. Von Korff, K. Saunders, W.M. Baluch, G.E. Simon. A chronic disease score with empirically derived weights. Medical Care, 33 (1995), pp. 783–795
3 R.E. Johnson, M.C. Hornbrook, G.A. Nichols. Replicating the chronic disease score (CDS) from automated pharmacy data. Journal of Clinical Epidemiology, 47 (1994), pp. 1191–1199
4 L.M. Lamers, R.C. van Vliet. The Pharmacy-based Cost Group model: validating and adjusting the classification of medications for chronic conditions to the Dutch situation. Health Policy, 68 (2004), pp. 113–121
5 M. Von Korff, E.H. Wagner, K. Saunders. A chronic disease score from automated pharmacy data. Journal of Clinical Epidemiology, 45 (1992), pp. 197–203
6 P.A. Fishman, M.J. Goodman, M.C. Hornbrook, R.T. Meenan, D.J. Bachman, M.C. O’Keeffe Rosetti. Risk adjustment using automated ambulatory pharmacy data: the RxRisk model. Medical Care (2003), pp. 84–99
7 J.S. Hughes, R.F. Averill, J. Eisenhandler, N.I. Goldfield, J. Muldoon, J.M. Neff, J.C. Gay. Clinical Risk Groups (CRGs): a classification system for risk-adjusted capitation-based payment and health care management. Medical Care, 42 (2004), pp. 81–90
8 G.E. Hanley, S. Morgan, R.J. Reid. Explaining prescription drug use and expenditures using the adjusted clinical groups case-mix system in the population of British Columbia, Canada. Medical Care, 48 (2010), pp. 402–408
9 R.N. Kuo, M.S. Lai. Comparison of Rx-defined morbidity groups and diagnosis-based risk adjusters for predicting healthcare costs in Taiwan. BMC Health Services Research, 10 (2010), p. 126
10 P.J. Stam, R.C. van Vliet, W.P. van de Ven. Diagnostic, pharmacy-based, and self-reported health measures in risk equalization models. Medical Care, 48 (2010), pp. 448–457
11 M. Caballer-Tarazona, I. Moya-Clemente, D. Vivas-Consuelo, I. Barrachina-Martínez. A model to measure the efficiency of hospital performance. Mathematical and Computer Modelling, 52 (2010), pp. 1095–1102
12 M. Caballer-Tarazona, L. Buigues-Pastor, I. Saurí- Ferrer, R. Uso-Talamantes, J.L. Trillo-Mata. A standardized amount indicator by equivalent patient to control outpatient pharmaceutical expenditure, Spain. Revista Espanola de Salud Pública, 86 (2011), pp. 371–380
13 L.M. Lamers. Health-based risk adjustment: is inpatient and outpatient diagnostic information sufficient. Inquiry, 38 (2001), pp. 423–431
14 M. Garcia-Goni, P. Ibern, J.M. Inoriza. Hybrid risk adjustment for pharmaceutical benefits. The European Journal of Health Economics, 10 (2009), pp. 299–308
15 M. Garcia-Goni, P. Ibern. Predictability of drug expenditures: an application using morbidity data. Health Economics, 17 (2008), pp. 119–126
16 E. De la Poza-Plaza, I. Barrachina, J. Trillo-Mata, R. Uso-Talamantes. Sistema de Prescripción y dispensación electrónica en la Agencia Valenciana de Salud. El Profesional de la Información 2011, 20 (2011), p. 9
17 D. Vivas, N. Guadalajara, I. Barrachina, J.L. Trillo, R. Uso, E. de-la-Poza. Explaining primary healthcare pharmacy expenditure using classification of medications for chronic conditions. Health Policy, 103 (2011), pp. 9–15
18 M. Berlinguet, C. Preyra, S. Dean. Comparing the value of three main Diagnostic-Based Risk-Adjustment Systems (DBRAS). Foundation CHSR, Ottawa, Ontario (2005)
19 WHO International Working Group for Drug Statistics Methodology. ATC/DDD classification (final). (2000)
20 C.O. Sullivan, R.Z. Omar, G. Ambler, A. Majeed. Case-mix and variation in specialist referrals in general practice. British Journal of General Practice, 55 (2005), pp. 529–533
21 R.Z. Omar, C. O’Sullivan, I. Petersen, A. Islam, A. Majeed. A model based on age, sex, and morbidity to explain variation in UK general practice prescribing: cohort study. BMJ, 337 (2008), p. a238
22 J.M. Inoriza, J. Coderch, M. Carreras, L. Vall-Llosera, M. Garcia-Goni, J.M. Lisbona, P. Ibern. Measurement of morbidity attended in an integrated health care organization. Gaceta Sanitaria, 23 (2009), pp. 29–37
23 Aguado, E. Guino, B. Mukherjee, A. Sicras, J. Serrat, M. Acedo, J.J. Ferro, V. Moreno. Variability in prescription drug expenditures explained by adjusted clinical groups (ACG) case-mix: a cross sectional study of patient electronic records in primary care. BMC Health Services Research, 8 (2008), p. 11
24 Y. Zhao, R.P. Ellis, A.S. Ash, D. Calabrese, J.Z. Ayanian, J.P. Slaughter, L. Weyuker, B. Bowen. Measuring population health risks using inpatient diagnoses and outpatient pharmacy data. Health Services Research, 36 (2001), pp. 180–193
Artículos completos
Impact of population morbidity on health care costs in a health district.
Análisis de costes en el Área de Imagen Médica de grandes hospitales españoles.
Predictability of pharmaceutical spending in primary health services using Clinical Risk Groups.
Pharmaceutical cost management in an ambulatory setting using a risk adjustment tool.
Is Health Related Quality of Life (HRQoL) a valid indicator for health systems evaluation?
Atención a mujeres inmigrantes en un programa de mediación intercultural en salud.
Modeling Spanish anxiolytic consumption: Economic, demographic and behavioral influences.
Sistema de prescripción y dispensación electrónica en la Agencia Valenciana de Salud.
Costes y procesos hospitalarios en neurología. Estudio en un hospital de referencia.
Claves para motivar y fidelizar a los médicos especialistas.
Máster en Gestión Sanitaria Online 2023/2024
Artículos completos en la web del CIEGS
Impact of population morbidity on health care costs in a health district.
Análisis de costes en el Área de Imagen Médica de grandes hospitales españoles.
Predictability of pharmaceutical spending in primary health services using Clinical Risk Groups.
Pharmaceutical cost management in an ambulatory setting using a risk adjustment tool.
Is Health Related Quality of Life (HRQoL) a valid indicator for health systems evaluation?
Atención a mujeres inmigrantes en un programa de mediación intercultural en salud.
Modeling Spanish anxiolytic consumption: Economic, demographic and behavioral influences.
Sistema de prescripción y dispensación electrónica en la Agencia Valenciana de Salud.
Incidencia y variabilidad de la incapacidad temporal por trastornos de ansiedad en la Comunidad Valenciana durante el 2009.
Costes y procesos hospitalarios en neurología. Estudio en un hospital de referencia.
Claves para motivar y fidelizar a los médicos especialistas.


